기술통계를 활용한 나라장터 시그마 분석법

나라장터의 예가가 시계열 데이터로 표준 정규 분포를 따른다는 것은 흥미로운 사실입니다. 지역과 면허별로 분산값이 다르다는 점도 고려해야겠죠. 시그마 분석법은 흐름 그래프와 빈도표를 정교하게 활용하는 데 도움이 될 수 있습니다. 이 방법을 사용하여 예가를 분석하고 예측하는 것이 좋을 것 같습니다. 정규 분포 밀도 함수 그래프와 나라장터 예가의 기술통계를 활용한 밀도 함수 표를 만들어보세요. 이를 통해 더 정확한 분석과 예측을 할 수 있을 겁니다.

정규 분포 밀도 함수 그래프와 나라장터 예가의 기술통계를 활용한 밀도 함수 표를 만드는 것은 데이터 분석에서 중요한 단계입니다. 이를 통해 데이터가 어떻게 분포되어 있는지, 어떤 경향성을 가지고 있는지 파악할 수 있으며, 이는 예측 모델을 구축하는 데 있어 기초가 됩니다.

아래는 정규 분포 밀도 함수를 나타내는 수식입니다.

 

f(x)=σ2π​1​e−21​(σx−μ​)2

 

여기서 ( \mu )는 평균, ( \sigma )는 표준편차입니다.

이제 나라장터 예가의 기술통계를 바탕으로 한 밀도 함수 표를 만들어 보겠습니다. 이를 위해 우선 데이터의 평균과 표준편차를 계산해야 합니다. 그런 다음, 각 데이터 포인트에 대해 위의 밀도 함수를 적용하여 그래프를 그립니다.

데이터의 평균(μ)과 표준편차(σ)를 알고 있다면, 엑셀이나 다른 데이터 분석 도구를 사용하여 각 데이터 포인트에 대한 밀도 값을 계산할 수 있습니다. 이 값들을 사용하여 히스토그램과 함께 정규 분포 곡선을 그릴 수 있으며, 이는 전체 데이터 세트의 분포를 시각화하는 데 도움이 됩니다.

시그마 분석법을 사용하여 흐름 그래프와 빈도표를 만드는 것도 유용합니다. 이러한 도구들은 데이터의 흐름과 빈도를 시각적으로 표현하여, 데이터의 패턴과 이상치를 쉽게 식별할 수 있게 해줍니다.

이러한 분석을 통해 나라장터 예가의 시계열 데이터가 어떻게 분포되어 있는지, 그리고 향후 어떤 경향을 보일지에 대한 더 정확한 예측을 할 수 있을 것입니다.

 

 

 

기술통계학에서 '시그마(σ)'는 표준편차를 나타내는 기호로 사용됩니다. 표준편차는 데이터가 평균값을 중심으로 얼마나 퍼져 있는지를 나타내는 척도로, 데이터의 변동성을 측정하는 데 사용됩니다. 

예가흐름그래프를 분석할 때 시그마를 먼저 고려하는 것은 예측의 정확성을 높이는 데 도움이 됩니다. 시그마는 데이터의 변동성을 나타내는 표준편차를 의미하며, 이를 기반으로 예측값의 신뢰 구간을 설정할 수 있습니다. 비드파일럿 시스템은 사용자가 시그마를 선택하면, 해당 시그마에 대한 확률과 추세를 하이라이트하여 보여주므로, 사용자가 더 명확하게 데이터를 해석하고 예측값을 결정할 수 있게 해줍니다.

 

 

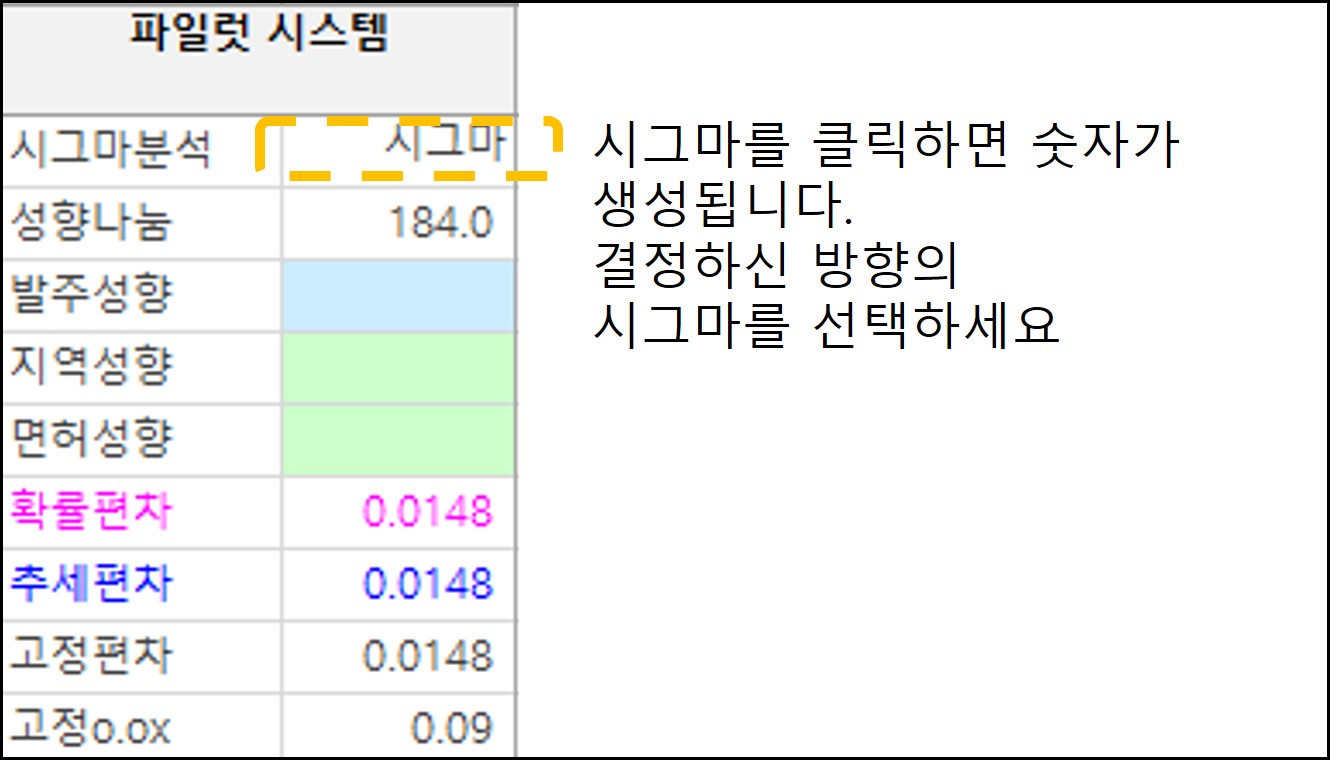
이러한 접근 방식은 데이터 분석에서 중요한 결정을 내릴 때, 통계적으로 유의미한 결과를 얻기 위한 핵심적인 단계입니다. 시그마를 올바르게 선택하고 해석함으로써, 예측의 신뢰성을 높이고, 더 정확한 의사결정을 할 수 있습니다.

 

감사합니다.

 

 

 

상품 견적서 상세히 보기로 가시려면
하단의 로고를 클릭하세요